![]()
ISSN 2379-5980 (online) DOI 10.5195/LEDGER.2022.260
RESEARCH ARTICLE
Coin Transfer Unlinkability Under the Counterparty Adversary Model
Takeshi Miyamae,∗† Kanta Matsuura‡
Abstract. Unlinkability is a crucial property of cryptocurrencies that protects users from deanonymization attacks. However, currently, even anonymous cryptocurrencies do not necessarily attain unlinkability under specific conditions. For example, Mimblewimble, which is considered to attain coin unlinkability using its transaction kernel offset technique, is vulnerable under the assumption that privacy adversaries can send their coins to or receive coins from the challengers. This paper first illustrates the privacy issue in Mimblewimble that could allow two colluded adversaries to merge a person’s two independent chunks of personally identifiable information (PII) into a single PII. To analyze the privacy issue, we formulate unlinkability between two sets of objects and a privacy adversary model in cryptocurrencies called the counterparty adversary model. On these theoretical bases, we define an abstract model of blockchain-based cryptocurrency transaction protocols called the coin transfer system, and unlinkability over it called coin transfer unlinkability (CT-unlinkability). Furthermore, we introduce zero-knowledgeness for the coin transfer systems to propose a method to easily prove the CT-unlinkability of cryptocurrency transaction protocols. Finally, we prove that Zerocash is CT-unlinkable by using our proving method to demonstrate its effectiveness.
![]()
∗ 1ERsMcmcaRCri5jYPJ8Tqbr93V9UFXk3eF
† T. Miyamae (miyamae.takeshi@fujitsu.com) is a senior researcher at Fujitsu Limited, Japan and a Ph.D. student at The University of Tokyo, Japan.
‡ K. Matsuura (kanta@iis.u-tokyo.ac.jp) is a professor at The University of Tokyo, Japan.
![]()
PII Linkability Issue via Mimblewimble Protocol—Unlinkability is a crucial property of cryptocurrencies that protects users from deanonymization attacks, as demonstrated by Bonneau et al., Amarasinghe et al., etc.;1,2 however, although Silveira et al. derived the conclusion that Mimblewimble protocol attains transaction unlinkability, the actual risks of cryptocurrency’s coin linkability are not necessarily understood.3–5 In this section, we illustrate a privacy issue via Mimblewimble protocol concerning personally identifiable information (PII).6
Let “Alice” be an employee of Fujitsuna Co., and be assigned an employee number. Her official PII, e.g., name, email address, phone number, address, ID photo, is recorded on the Fujitsuna Co.’s employee database. Because Fujitsuna Co. is a high-technology company, they pay the salaries of their employees using Beam,7 one of the Mimblewimble-based cryptocurrencies.3
On the other hand, let Alice privately enjoy a content distribution service operated by Tsutayama Movie Contents (TMC) Co. She is assigned her user ID. Her private PII, e.g., private
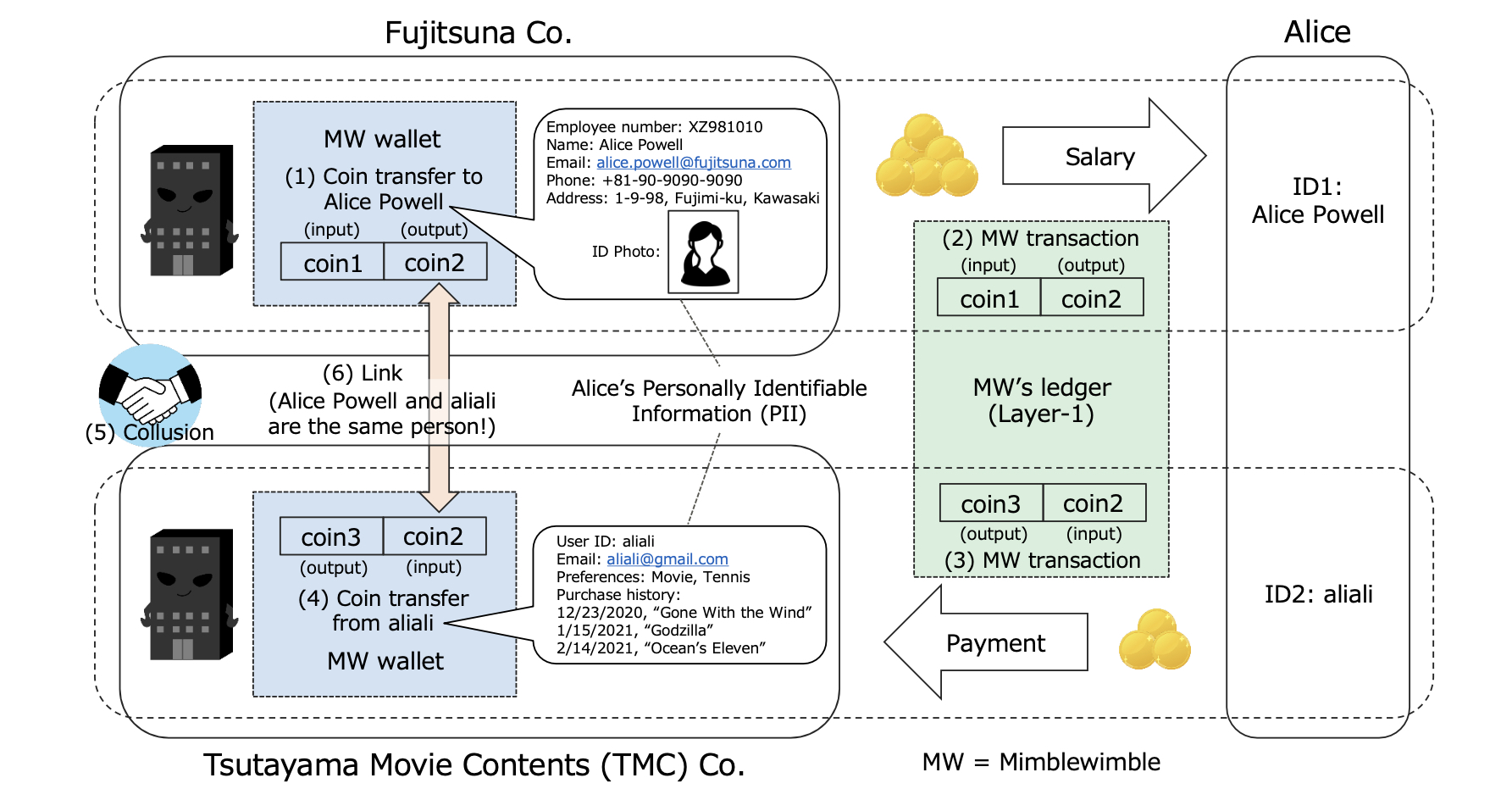
Fig. 1. PII Linkability Issue via Mimblewimble
email address, preferences including hobbies, and purchase history, is recorded on the TMC Co.’s customer database. Since TMC Co. is also a high-technology company, they support Beam as a payment means.
In most Mimblewimble-based cryptocurrencies, both the sender and the recipient of a trans- action know all identifiers of input coins and output coins. As shown in Figure 1, Fujitsuna Co. and Alice know the identifiers of coin1 and coin2, while Alice and TMC Co. know the identifiers of coin2 and coin3. Therefore, if Fujitsuna Co. and TMC Co. colluded, they could associate Alice’s official PII in Fujitsuna Co. with her private PII in TMC Co. via the identifier of coin2. That is, Fujitsuna Co. could grasp Alice’s private information, e.g., her hobbies and purchase history of movies, which is one of the privacy risks caused by Mimblewimble’s insufficient coin unlinkability. However, this kind of issue has never been thoroughly discussed, and no solutions have ever been proposed so far. This is mainly because the sender and the recipient in a coin transfer are assumed to trust each other in most existing privacy adversary models.
In this study, we introduce the counterparty adversary model and coin transfer unlinkability (CT-unlinkability) to analyze the PII unlinkability via any kind of cryptocurrency transaction protocols.
Related Work—Pfitzmann et al. systematically defined the unlinkability of two or more items of interest (IOIs) for general communication protocols.8 Some cryptocurrency researchers, e.g., Amarasinghe et al., noticed that cryptocurrency transactions can also be handled in the same way as the messages in the communication protocols, and they attempted to apply the Pfitzmann’s unlinkability to their analysis of cryptocurrency’s privacy properties.2 However, the application of the Pfitzmann’s unlinkability does not seem reasonable because it is defined as a relation among the same kind of objects in a set (e.g., message senders), while we would like to handle the relation between general objects (e.g., a relation between a sender and a transaction). Backes et al. proposed AnoA framework for defining, analyzing, and quantifying anonymity properties, including sender unlinkability, for anonymous communication (AC) protocols, using computational differential privacy.9 They modeled the AC protocols, generalized the notion of computational differential privacy (CDP) to apply it to the AC protocols, and analyzed the privacy of the AC protocols. However, since their theory assumes simple messaging that only includes a sender, a recipient, and auxiliary information (that corresponds to layer-0 in blockchain protocol layers), it is difficult for us to apply it to cryptocurrency transaction protocols (that correspond to layer-1 and layer-2).
In the research field of cryptocurrency, Androulaki et al. defined activity unlinkability and user profile indistinguishability to analyze the privacy of cryptocurrencies including Bitcoin.10,11 Activity unlinkability assesses the difficulty of identifying whether two different addresses or transactions belong to the same user. User profile indistinguishability assesses the adversary’s ability to group the addresses and transactions of the same user. However, since their definitions only focus on the unlinkability (or indistinguishability) between addresses or transactions, they cannot handle unlinkability between general objects including coins. Furthermore, since it assumes that the challengers never share any secret information with the adversaries, it cannot be applied to the privacy issue under the counterparty adversary model defined in our work.
Ben-Sasson et al. defined ledger indistinguishability in their Zerocash paper to assess the unlinkability between the transactions on the ledger of their decentralized anonymous payment (DAP) scheme and the honest parties who participate in the DAP scheme.12 The adversary can adaptively induce the honest parties to perform DAP operations of his choice. However, since they assume that the counterparties of each challenger are not included in their adversaries and that the private information of each coin is always hidden on the challenger’s side, their privacy adversary model is not realistic. Furthermore, since the challenger’s APIs are largely specific to the DAP scheme, their ledger indistinguishability is only applicable to Zerocash or its close relatives.
Silveira et al. defined transaction unlinkability in their formulation of Mimblewimble.3 They claim using the definition that since transaction kernel offsets are added to generate a single block kernel offset, Mimblewimble attains transaction unlinkability. However, the scheme is specific to the confidential transactions and the claim is only applicable to Mimblewimble.13
In the research field of cryptography, a large number of zero-knowledge proof system protocols have been proposed based on the simulation paradigm.14–16 These protocols have made a significant contribution to enhancing privacy in various fields including anonymous cryptocurrencies. However, the application of the simulation paradigm in any other field than zero-knowledge proof systems has been unusual so far.
Contents—The remainder of this paper is organized as follows. In Section 2, we formulate unlinkability between two sets of objects. In Section 3, we define a privacy adversary model in cryptocurrencies called the counterparty adversary model. In Section 4, we define an abstract model of blockchain-based cryptocurrency transaction protocols called the coin transfer system, and unlinkability over it called coin transfer unlinkability (CT-unlinkability) under the counterparty adversary model. In Section 5, we introduce zero-knowledgeness for the coin transfer systems to propose a method to easily prove the CT-unlinkability of cryptocurrency transaction protocols. In Section 6, we prove that Zerocash is CT-unlinkable by using our proving method to demonstrate its effectiveness. Section 7 concludes the paper.
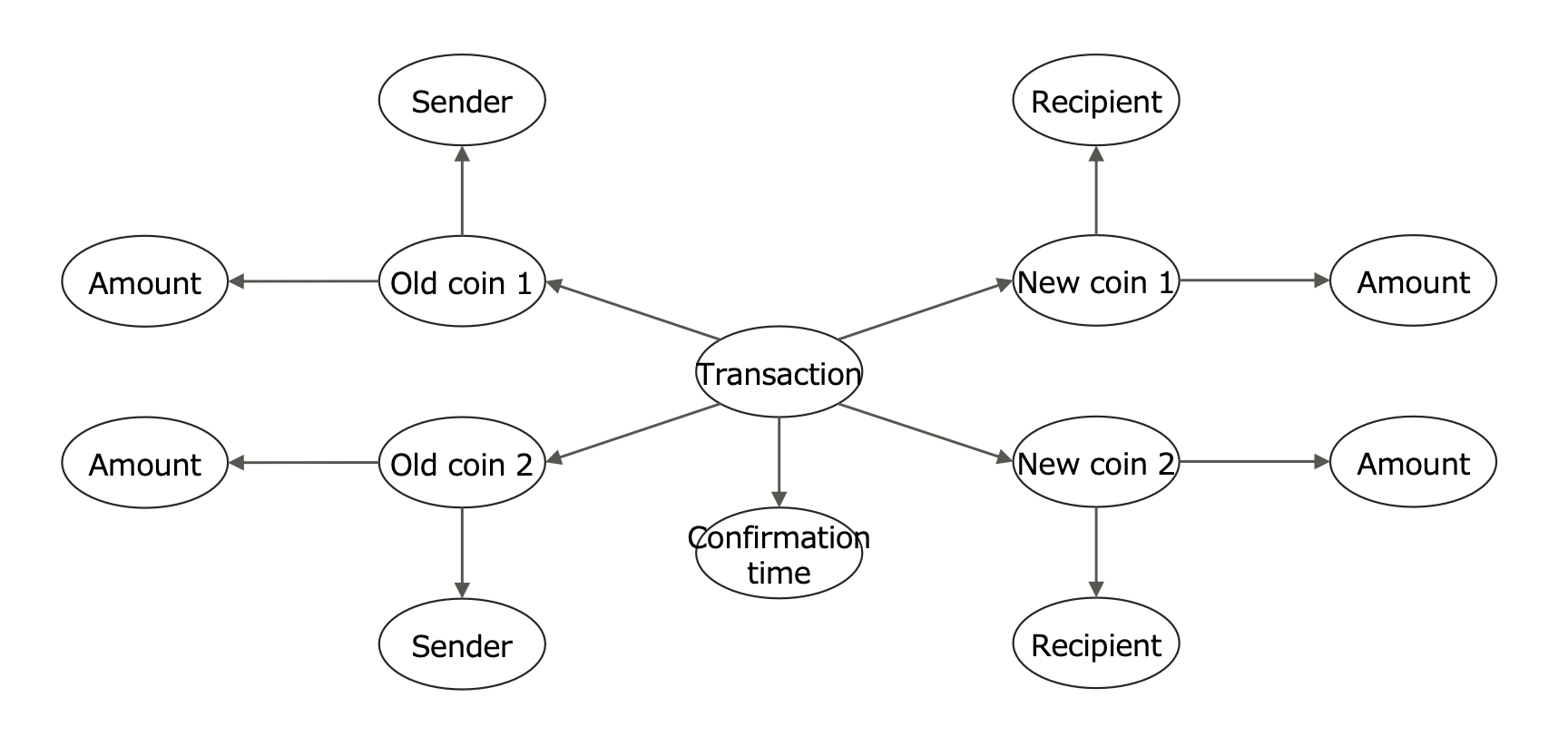
Fig. 2. Cryptocurrency Transaction Information Model
This section formulates unlinkability between two sets of objects.
Cryptocurrency Transaction Information Model—First, we introduce an object graph that represents a typical transaction information of UTXO-style cryptocurrency in Figure 2. Everyone instantly notices that the transaction sender and the transaction recipient are linkable if a cryptocurrency is designed to be perfectly transparent as Bitcoin is. In contrast, most anonymous cryptocurrencies try to hide the link between the sender and the recipient. If it is difficult to show the association between the sender and the recipient, we informally call it unlinkable.
Object—We define a notion called object as the most fundamental element of the cryptocurrency transaction information model, over which we formally define several privacy properties in cryptocurrencies. An object is defined as information because blockchain-based cryptocurrencies are implemented as software.
Definition 1 (Object). An ‘object’ is a primitive piece of information that indicates someone or something in a cryptocurrency.
For example, a transaction, a sender, a recipient, an old coin, a new coin, coin amount, and transaction confirmation time are the objects in a typical UTXO-style cryptocurrency.
Attribute—We define a notion called attribute to introduce a fundamental relation between objects.
Definition 2 (Attribute). An ‘attribute’ is an object that indicates a property of an original object. We also call the attribute a ‘child’ of the original object and call the original object a ‘parent’ of the attribute.
For example, an old coin is an attribute of a transaction, and a sender is an attribute of an old coin in a typical UTXO-style cryptocurrency.
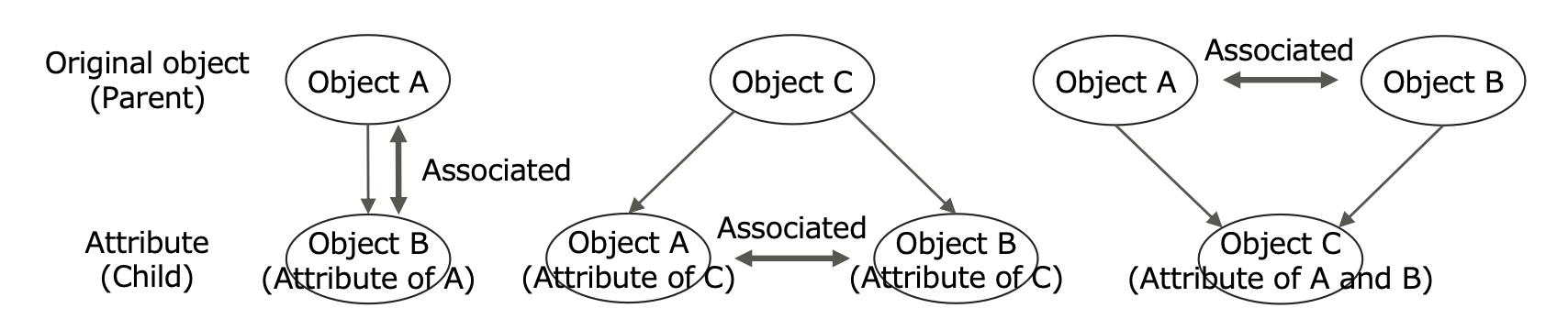
Fig. 3. Object, Attribute, and Association
Association—We define another notion of relation called association that does not contain any hierarchical relationship between objects.
Definition 3 (Association). Let O be a set of objects. If A ∈ O and B ∈ O satisfy either of the following conditions from the perspective of a participant (e.g., an adversary), we call the relation between A and B ‘A and B are associated.’ (We define a boolean function Assoc : O2 → {0, 1} as Assoc(A, B) = 1 if and only if A and B are associated.)
A is an attribute of B, or B is an attribute of A.
Both A and B are attributes of an identical parent object.
Both A and B have an identical child attribute object.
There exists C ∈ O wherein Assoc(A,C) = 1 and Assoc(B,C) = 1.
Note that the relation defined in Definition 3 is also expressed as ‘A is associated with B’ or ‘B is associated with A.’ If A and B are not associated, then we call the relation ‘A and B are unassociated.’
For example, a sender is associated with a sent coin because the sender is an attribute of the sent coin. A coin sent by a sender to Alice and a coin sent by the identical sender to Bob are associated because both the coin sent to Alice and the coin sent to Bob have an identical sender. We illustrate these notions for the cryptocurrency transaction information model (object,
Unlinkability—We define unlinkability in this section, which is the essential privacy property in cryptocurrencies.
Definition 4 (Unlinkability). Let O be a set of objects. Given a set of objects of an identical type A = {Ai|i = 0, ..., n − 1} ⊂ O and another set of objects of another identical type B = {Bj| j = 0, ..., m − 1} ⊂ O, where A ∩ B = ∅ .∗ If the adversary A’s advantage of the indistinguishability game Gassoc(nsec)(A, B) where nsec is a security parameter (e.g. key length), adv(Gassoc(nsec)(A, B)) = max(|Pr[b = bt]–1/2|), is negligible, then we call the relation between A and B ‘A and B are unlinkable.’
Challenger C : randomly selects a pair of objects p0 = (Ae ∈ A, Bq ∈ B) where Assoc(Ae, Bq) = 1, randomly selects another pair of objects p1 = (Af ∈ A, Bs ∈ B) where Assoc(Af , Bs) = 0, randomly selects b ← {0, 1}, and sends Pb to A according to the value of b where P0 = (p0, p1) and P1 = (p1, p0).
Adversary A : guesses bt ← {0, 1} where Pbt was sent by C .
![]()
∗ We assume that at least one pair of objects are associated and at least another pair of objects are unassociated.
![]()
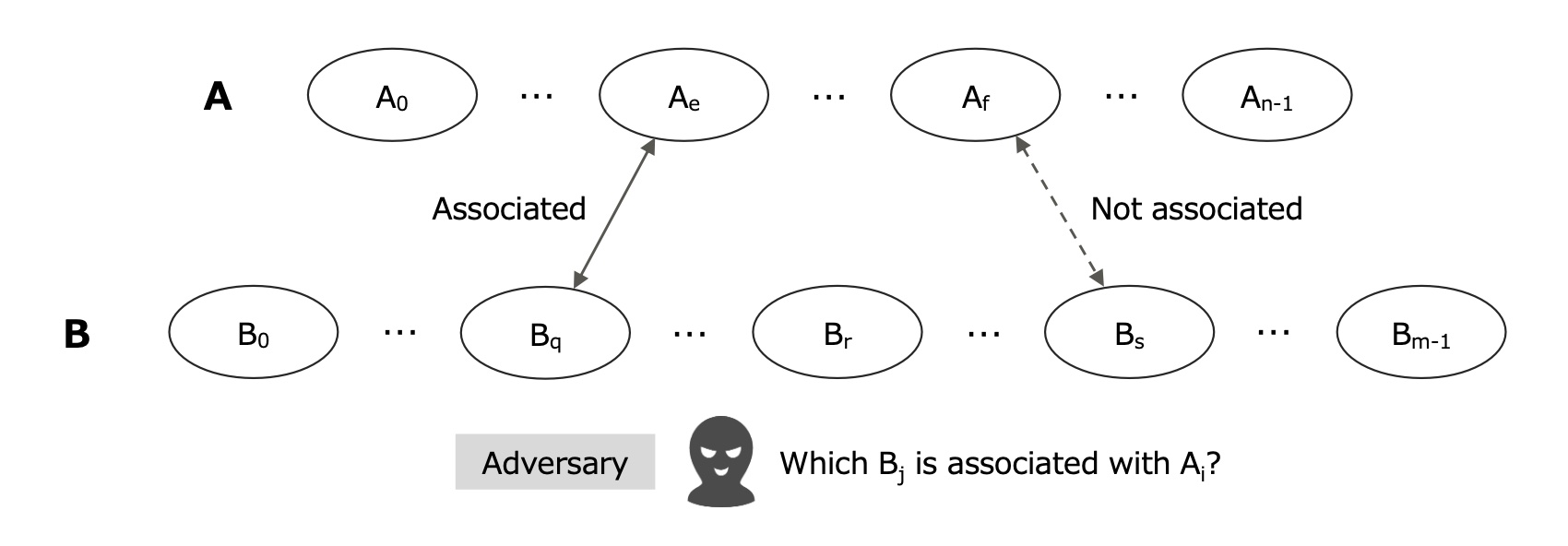
Fig. 4. Indistinguishability Game Gassoc(A, B) for Unlinkability
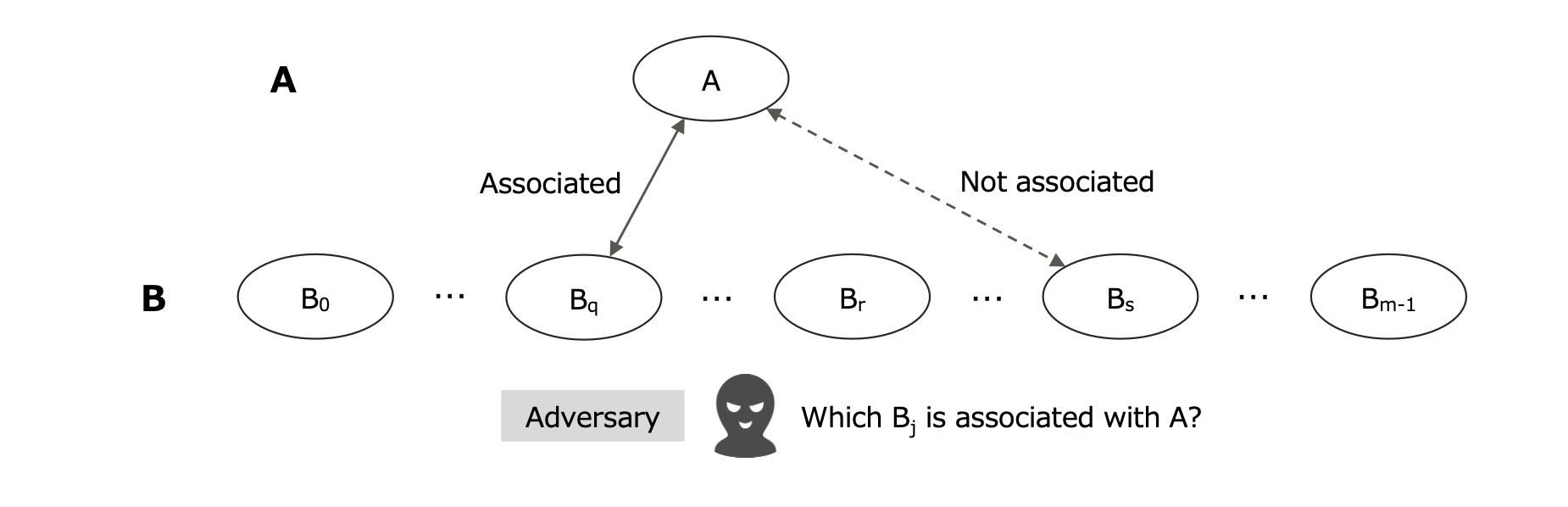
Fig. 5. Indistinguishability Game Gassoc(A = {A}, B) for Object Unlinkability
For example, B = {cmi | all the coin commitments on the ledger} is unlinkable with A ={addri | all the possible recipient addresses} in Zerocash because adversaries cannot guess who is the recipient of each coin commitment.12
On the other hand, B = {cmi | all the coin descriptors (UTXO transaction outputs) on the ledger} is linkable with A = {addri | all the possible recipient addresses} in Bitcoin because every relation between a coin and its recipient is disclosed in the coin descriptor and anyone can see it.11
Definition 5 (Object Unlinkability). If A contains only a single object A (A = {A}), then Definition 4 defines ‘object unlinkability’ between A = {A} and B using the indistinguishability game Gassoc(A = {A}, B).
For example, A (= a recipient address) is unlinkable with B ={cmi | all the coin commitments on the ledger} in Zerocash. Conversely, A (= a coin commitment) is unlinkable with B = {addri | all the possible recipient addresses} in Zerocash.
Theorem 2.1 (Transitivity of Unlinkability). Unlinkability is a transitive relation.
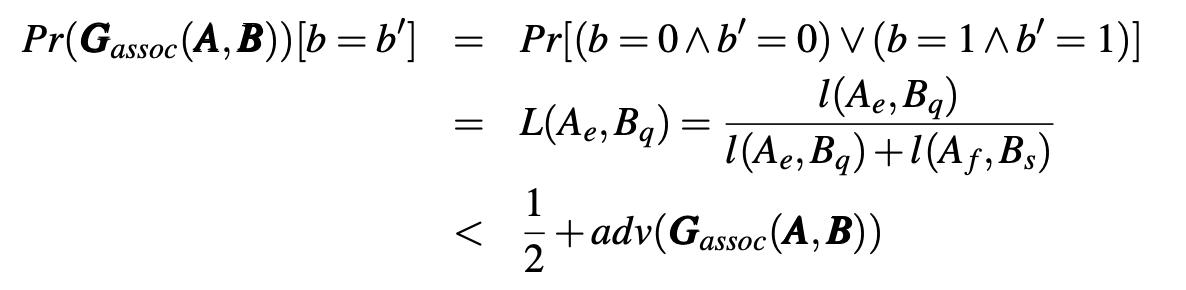
that is,
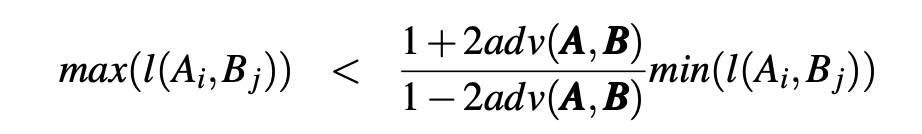
where l(Ai, Bj) is the likelihood that Bj is associated with Ai from the adversary’s perspective, and L(Ai, Bj) is the conditional likelihood that Bj is associated with Ai from the adversary’s perspective after they are sent Pb in the indistinguishability game Gassoc(A, B).
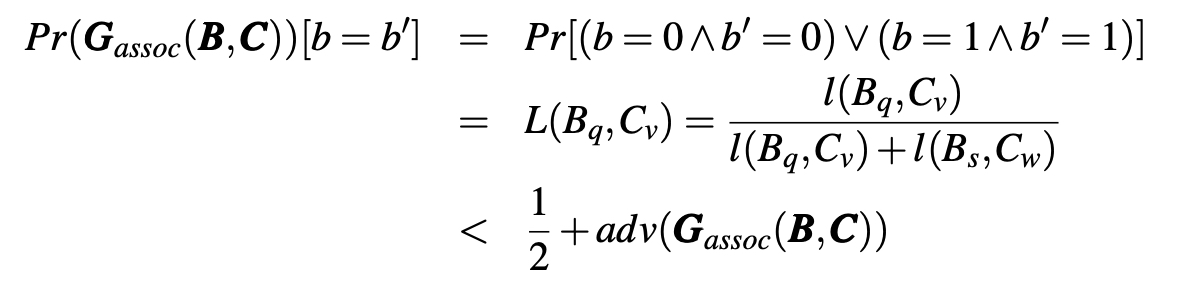
that is,
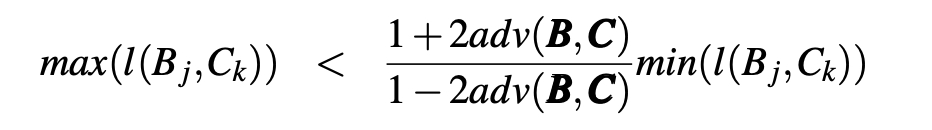
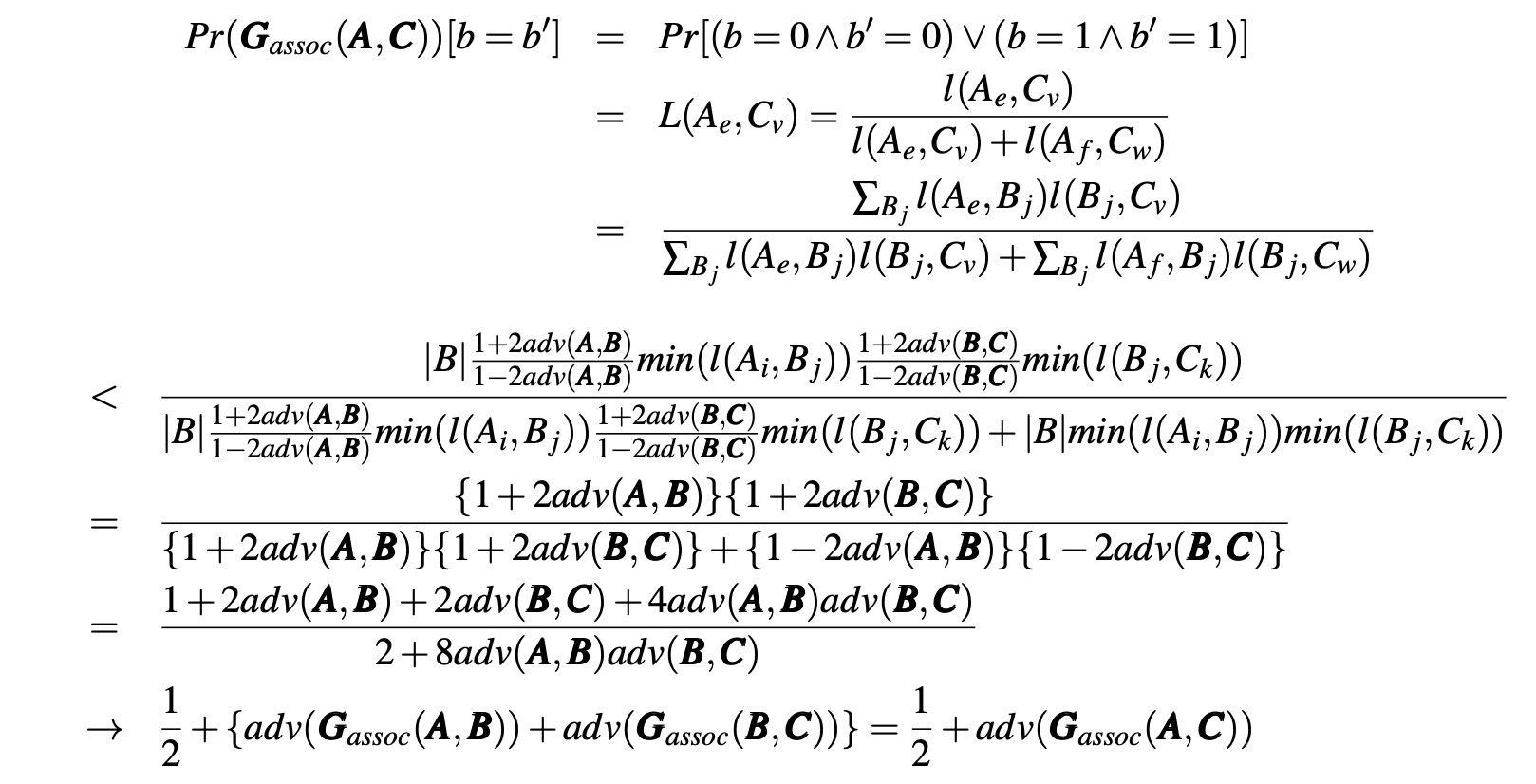
Hence, A and C are unlinkable (unlinkability is a transitive relation). Q.E.D.
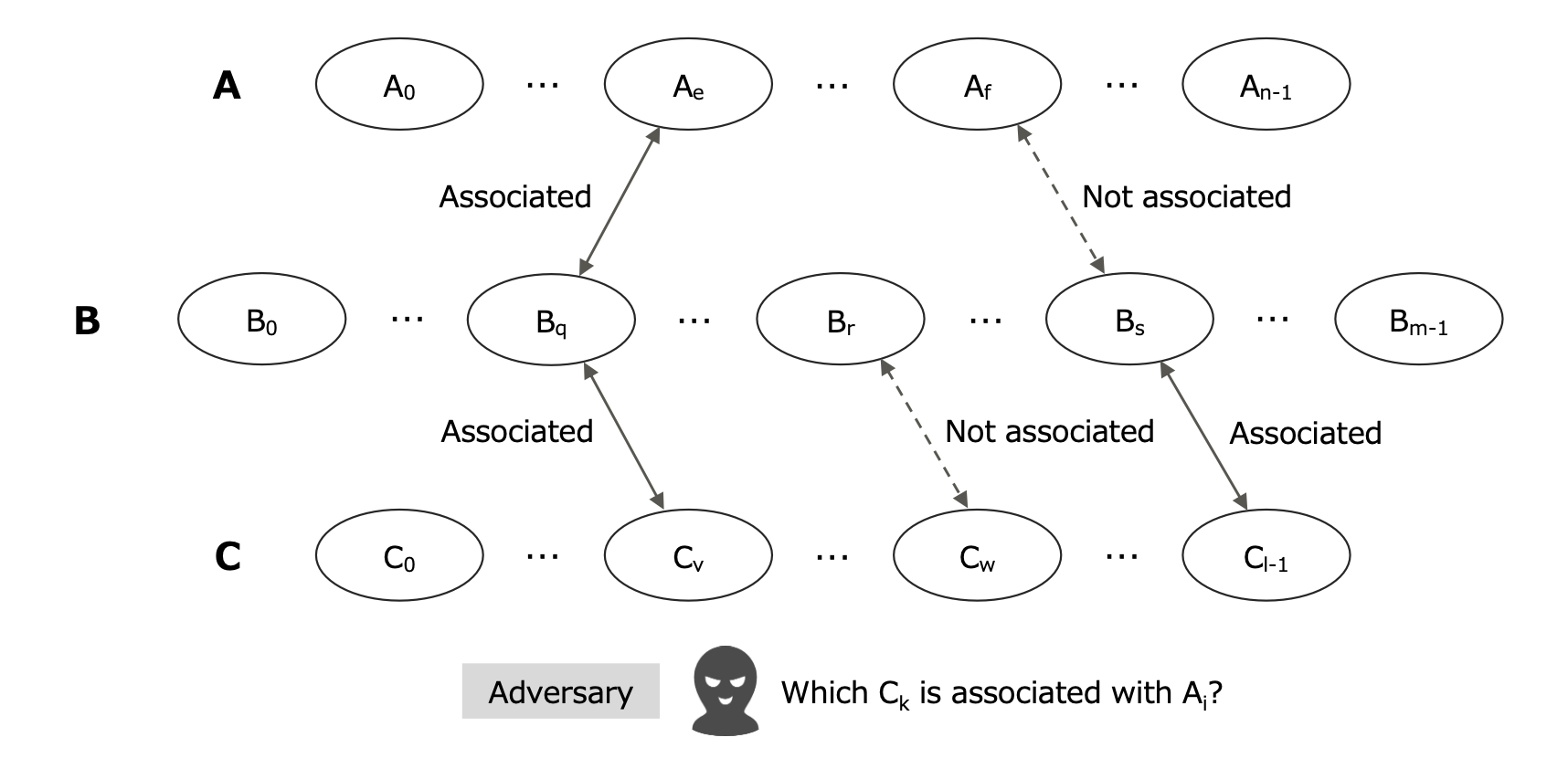
Fig. 6. Indistinguishability Game Gassoc(A, C) to Prove the Transitivity of Unlinkability
From this result, we only have to focus on the unlinkability in each information layer to achieve the entire unlinkability over the whole cryptocurrency transaction information model.
In this section, we define a privacy adversary model in cryptocurrencies called the counterparty adversary model, where we assume that the counterparties of each challenger in coin transfer transactions can become their privacy adversaries.
Current Privacy Adversary Model—Most of the past cryptocurrency studies have assumed that the counterparties of any challengers in coin transfer transactions never become their privacy adversaries.
The following two simple rules are assumed in the current privacy adversary model (see Figure 7).
The adversaries may not send their coins to the challengers.
The challengers may not send their coins to the adversaries.
As a result, the adversaries can only observe the coin transfer transactions between the challengers as privacy attacks. They cannot share any secret transaction information with the challengers.
Counterparty Adversary Model—On the other hand, we propose another privacy adversary model in cryptocurrencies, which does not assume either rule defined in Section 3.1 (see Figure 8). We call it the counterparty adversary model. In this privacy adversary model, since the adversaries can send their coins to or receive coins from the challengers, they can observe the challengers’ privacy using their shared secrets, in addition to the coin transfer observation.
The counterparty adversary model is highly reasonable because the real world is not split cleanly into two domains as shown in the current privacy adversary model. However, the counterparty adversary model has never been thoroughly discussed so far. Therefore, we must estimate the privacy threat from the counterparties during coin transfers to use cryptocurrencies as everyday payment means.
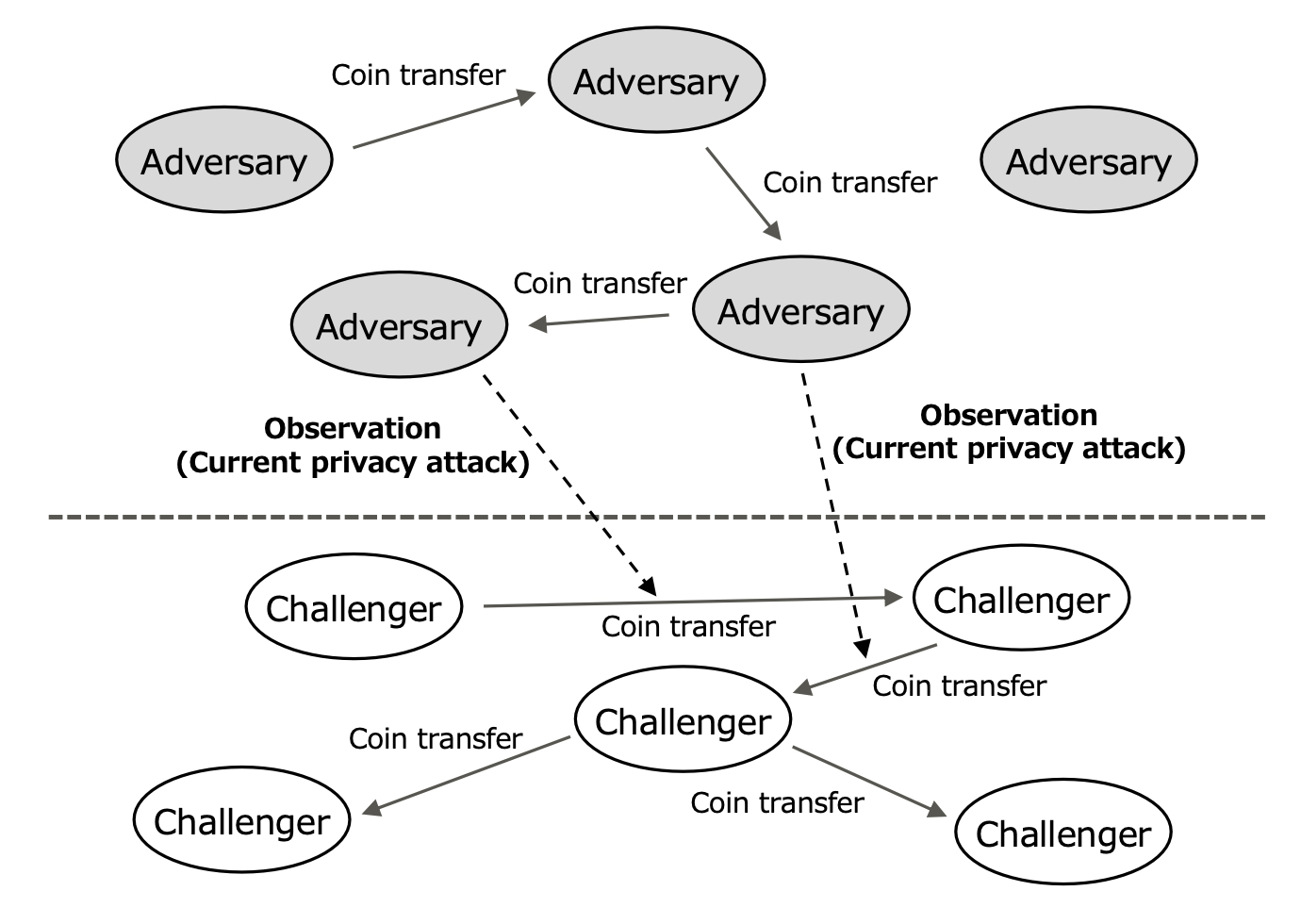
Fig. 7. Current Privacy Adversary Model
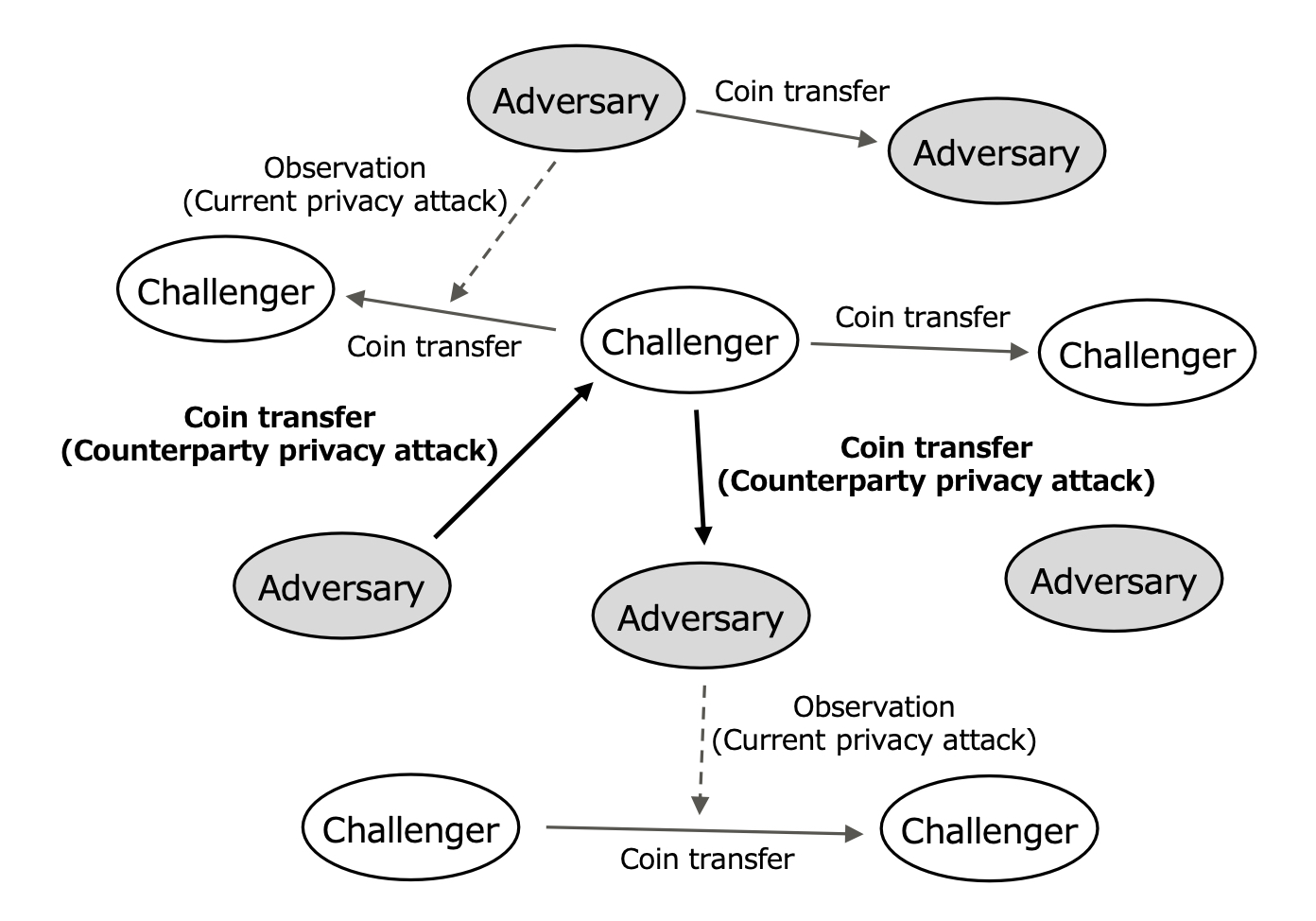
Fig. 8. Counterparty Adversary Model
PII Unlinkability—For example, we define a privacy issue that only occurs under the counterparty adversary model, called PII unlinkability (Figure 9). We consider a case that an adversary A1 sends a coin to a challenger C1, and C1 sends a coin using another identity C2 to another adversary A2. Even if A1 and A2 colluded with each other and they shared the C1’s PII and the C2’s PII with each other, a perfect privacy-enhancing coin transfer would keep the shared these PIIs unlinkable.† Conversely, if A1 and A2 colluded with each other and the coins that A1 sent to C1 and the coins that C2 sent to A2 were linkable, the adversaries could conclude that both identities C1 and C2 belong to an identical person. They could merge the C1’s PII and the C2’s PII into a single PII.
![]()
† We assume that the C1’s PII and the C2’s PII have no common part.
![]()
In this section, we define an abstract model of blockchain-based cryptocurrency transaction protocols called the coin transfer system, and unlinkability over it called coin transfer unlinkability (CT-unlinkability) under the counterparty adversary model.
Definition 6 (Coin Transfer System). Let M be a set of probabilistic polynomial-time Turing machines. M is a ‘coin transfer system’ if every machine Mf rom ∈ M can transfer their ownership of the coin to any other machine Mto ∈ M using a public information channel and a private information channel between them. We call each M ∈ M a ‘coin transfer machine.’
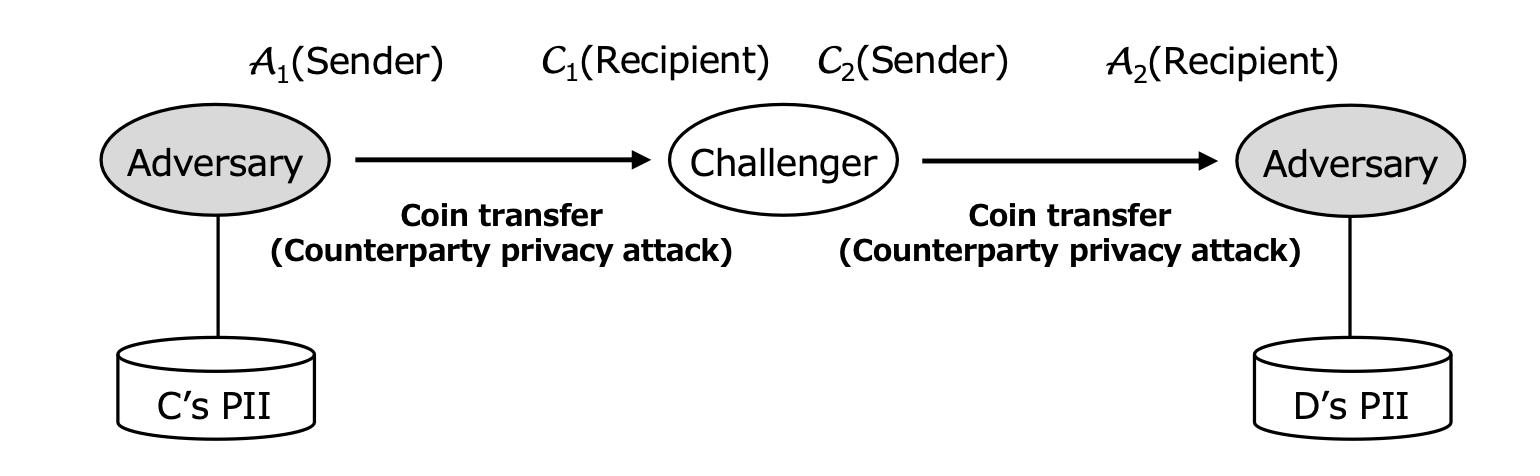
Fig. 9. PII Unlinkability
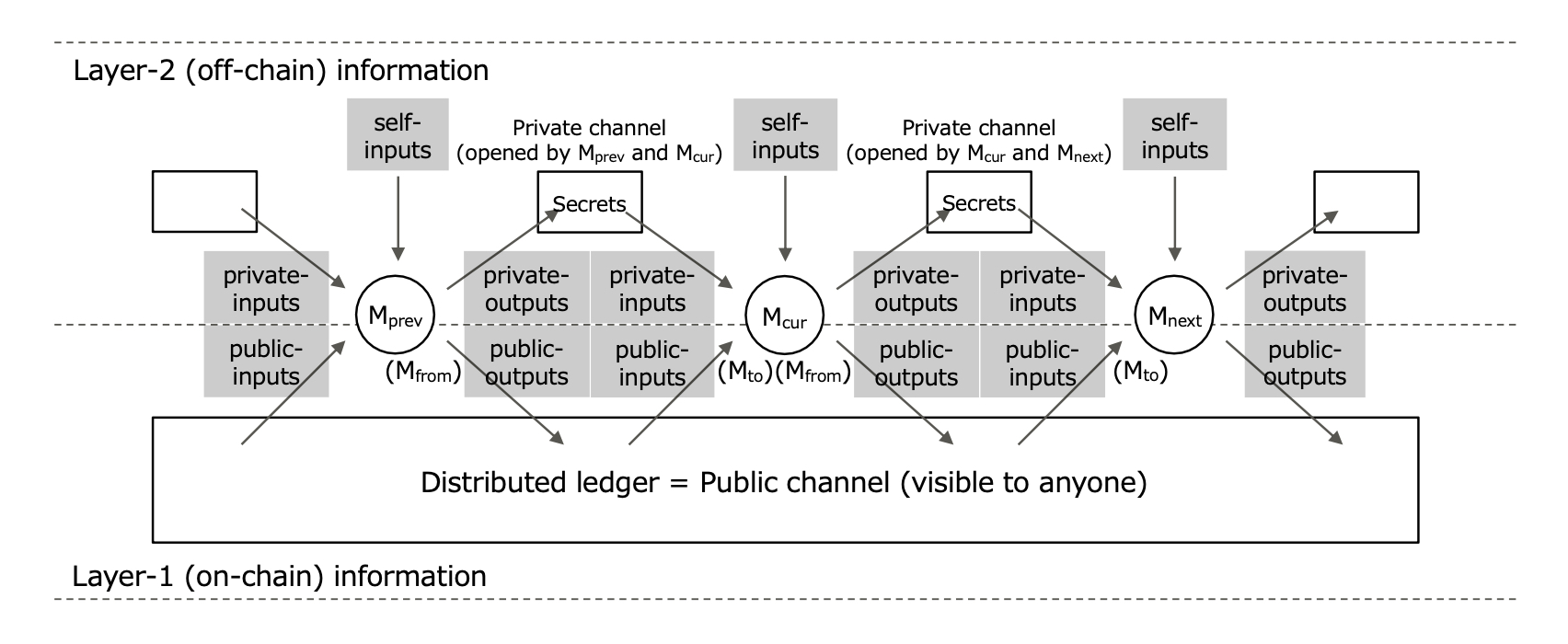
Fig. 10. Coin Transfer System
Note that a probabilistic polynomial-time algorithm means a probabilistic algorithm that always (i.e., independently of the outcome of its internal coin tosses) halts after a polynomial (in the length of the input) number of steps. The adversary’s verdict of whether to accept or reject the unlinkability is probabilistic, and a bounded error probability is allowed.
For example, a coin transfer system for blockchain-based cryptocurrencies is illustrated in Figure 10. Every blockchain-based cryptocurrency, including Bitcoin, uses a distributed ledger as a public information channel. Furthermore, most anonymous cryptocurrencies provide their protocols, including private channels between each participant.
Focusing on a machine Mcur, which is sent coins from Mprev and sends the sent coins to Mnext, its inputs are classified into three types, public-inputs (from the ledger), private-inputs (from Mprev), and self-inputs (e.g., random value generated by Mcur). On the other hand, its outputs are classified into two types, public-outputs (to the ledger) and private-outputs (to Mnext). This transaction process is denoted as a function named Mcur, such as (public-outputs, private-outputs to Mnext) = Mcur(public-inputs, private-inputs from Mprev, self-inputs).
Next, we introduce unlinkability in coin transfer systems under the counterparty adversary model.
Definition 7 (Coin Transfer Unlinkability). Given a coin transfer system defined in Definition 6 and a pair of colluding adversaries Mprev and Mnext. If all the coins sent by Mprev to the addresses other than Mprev and Mnext, denoted as Cout, and all the coins sent by the addresses other than Mprev and Mnext to Mnext, denoted as Cin, are unlinkable (regarding the association such that one coin is spent by another), we call the relation between Cout and Cin ‘coin transfer unlinkable (CT-unlinkable).’
The CT-unlinkability defined in Definition 7 is essential under the counterparty adversary model because it ensures PII unlinkability shown in Figure 9.
Theorem 4.1 (PII unlinkability under CT-unlinkability). CT-unlinkability ensures PII unlinkability.
[ Proof. ] Assuming that Cout and Cin are CT-unlinkable and that the C1’s PII and the C2’s PII are linkable by any coin transfers, at least one coin sent by adversary A1 to C1 and another coin sent by C2 to adversary A2 seems to be associated, which means that Cout and Cin are CT-linkable. This situation is a contradiction, so the assumption must be false. Therefore, if Cout and Cin are CT-unlinkable, the C1’s PII and the C2’s PII are also unlinkable by any coin transfers. Q.E.D.
This section introduces zero-knowledgeness for the coin transfer systems to propose a method to easily prove the CT-unlinkability of cryptocurrency transaction protocols.
It is relatively easy to prove that a certain cryptocurrency is CT-linkable because in such cases we only have to show at least one counterexample in which the adversary wins. In contrast, it is much more difficult to prove CT-unlinkable because we have to show that there are no examples. To show the CT-unlinkability easily, we introduce zero-knowledgeness using the simulation paradigm for the coin transfer systems similarly for zero-knowledge proof systems.17
Definition 8 (Computational Zero-Knowledge Coin Transfer System). Let M be a coin transfer system, Lpub be the set of all the possible public-inputs of M, and Lprv be the set of all the possible private-inputs of M. We say that M is ‘computational zero-knowledge’ (or just ‘zero-knowledge’) if for every probabilistic polynomial-time coin transfer machines Mprev, Mcur, Mnext ∈ M there exists a probabilistic polynomial-time algorithm M∗ that does not use private-inputs from Mprev, such that the following two ensembles are computationally indistinguishable:
{(public-outputs, private-outputs to Mnext) = Mcur(public-inputs, private-inputs from Mprev, self-inputs)}public-inputs∈Lpub,private-inputs∈Lprv (i.e., the output of the coin transfer machine Mcur after receiving coins from the coin transfer machine Mprev on public-inputs)
{(public-outputs, private-outputs to Mnext) = M∗(public-inputs, private-inputs from Mprev, self-inputs)}public-inputs∈Lpub,private-inputs∈Lprv (i.e., the output of the algorithm M∗ on public-inputs) Algorithm M∗ is called a ‘computational simulator’ (or just ‘simulator’) for the transformation Mcur of the private-inputs from Mprev.
The simulation paradigm works as a proving method to show that a participant has never been informed of any knowledge from the protocol. In the case of Definition 8, the existence of the simulator M∗ shows that no new association knowledge between cryptocurrency objects is leaked from Mcur to Mnext.
We also define an additional property called universality for zero-knowledge coin transfer systems.
Definition 9 (Universal Zero-Knowledge Coin Transfer System). Let M be a (computational) zero-knowledge coin transfer system. Suppose a simulator M∗ is only dependent on its self-inputs, and thus can be used for all Mcur ∈ M. In that case, we call M∗ a universal simulator, and we call M a universal zero-knowledge coin transfer system.
Here, we obtain a theorem that easily proves that a certain cryptocurrency is CT-unlinkable.
Theorem 5.1 (CT-Unlinkability of Universal Zero-knowledge Coin Transfer Systems). Universal zero-knowledge coin transfer systems are CT-unlinkable.
[ Proof. ] Let M be a universal zero-knowledge coin transfer system, Mprev, Mnext ∈ M be the adversaries of the CT-unlinkability indistinguishability game who collude with each other, and thus {Mi|Mi ∈ M, Mi /= Mprev, Mi /= Mnext} be the challengers of this game. Let a coin cassoc ∈ Cin that is associated with a coin sent by Mprev be sent by Massoc, and a coin cnassoc ∈ Cin that is not associated with any coin sent by Mprev be sent by Mnassoc. Since M is universally zero-knowledge, Massoc and Mnassoc can use the same simulator M∗ that is only dependent on its self-inputs. Therefore, the outputs of Massoc and the outputs of M∗ are indistinguishable, while the outputs of Mnassoc and the outputs of M∗ are also indistinguishable. Therefore, the outputs of Massoc and the outputs of Mnassoc are indistinguishable, meaning that the adversaries cannot win the CT-unlinkability indistinguishability game. Thus M is CT-unlinkable. Q.E.D.
In this section, we first prove that Mimblewimble is CT-linkable. Next, we prove that Zerocash is CT-unlinkable by using our proving method to demonstrate its effectiveness.
Mimblewimble—Mimblewimble is one of the major anonymous cryptocurrency transaction protocols that has already been implemented in Grin and Beam, and later formulated by Silveira et al.3–5,7,18 Owing to the transaction kernel offset, Mimblewimble can shuffle the transaction outputs and attain coin unlinkability, as shown in ValueShuffle and the Silveira et al.’s formulation (ValueShuffle also proposes a decentralized protocol using secure multi-party computation).19 Therefore, it is difficult for the adversaries under the current privacy adversary model to find any association between input coins (e.g., coin1 in Figure 11) and output coins (coin2).
However, under the counterparty adversary model, a sender adversary Mprev can know the association between the input coins (coin1) sent by the adversary Mprev and the output coins (coin2) received by a challenger Mcur. Similarly, a receiver adversary Mnext can know the association between the input coins (coin2) sent by a challenger Mcur and the output coins (coin3) received by the adversary Mnext. Therefore, in the CT-unlinkability indistinguishability game adversaries can easily distinguish whether each coin sent by the sender adversary was spent for another coin received by the receiver adversary or not, which means that the adversaries’ advantage in the indistinguishability game is not negligible. Thus, we conclude that Mimblewimble is CT-linkable.
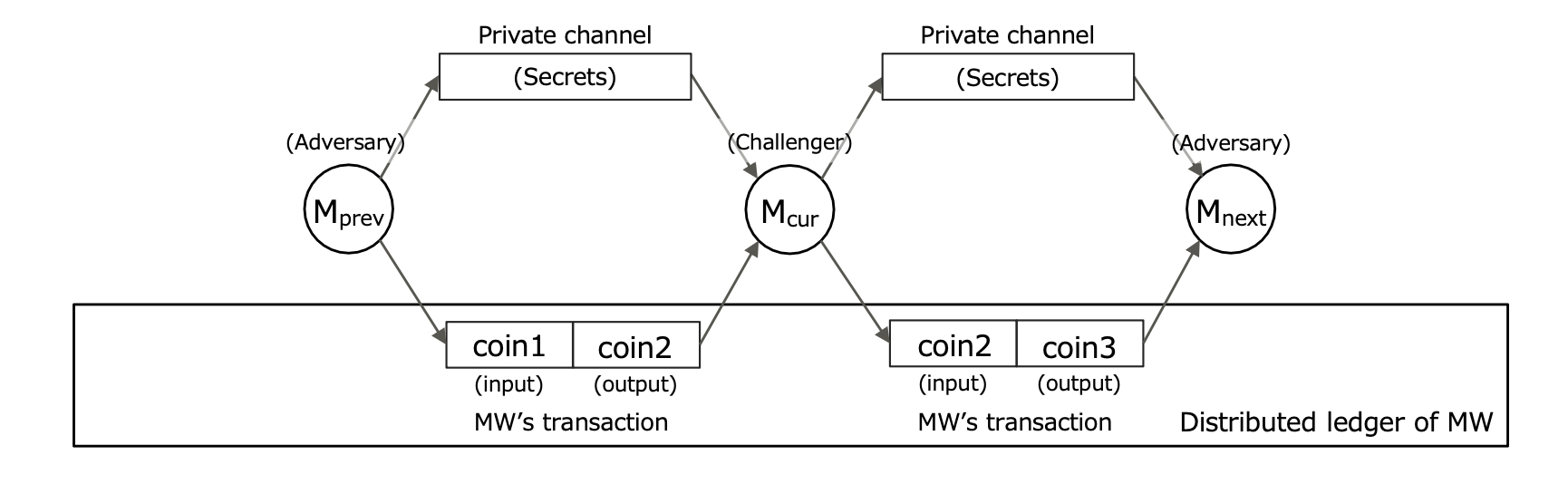
Fig. 11. Mimblewimble Coin Transfer System
Zerocash—Zerocash is one of the most sophisticated anonymous cryptocurrencies and has already been implemented in Zcash.12,20 First, we briefly illustrate the anonymization scheme in Zerocash.
In Zerocash, all coins on the ledger are encrypted. Two seemingly unrelated identifiers, a coin commitment cm and a serial number sn (Figure 12), are used to identify each coin. A transaction sender uses cmnew as an identifier of the coin (described as cnew from the viewpoint of the sender). In contrast, a corresponding transaction recipient uses snold as another identifier of the same coin (described as cold from the viewpoint of the recipient). Consequently, this makes the two identifiers of the same coin recorded in the shared ledger unlinkable even from the sender (only the recipient can link those two coin identifiers).
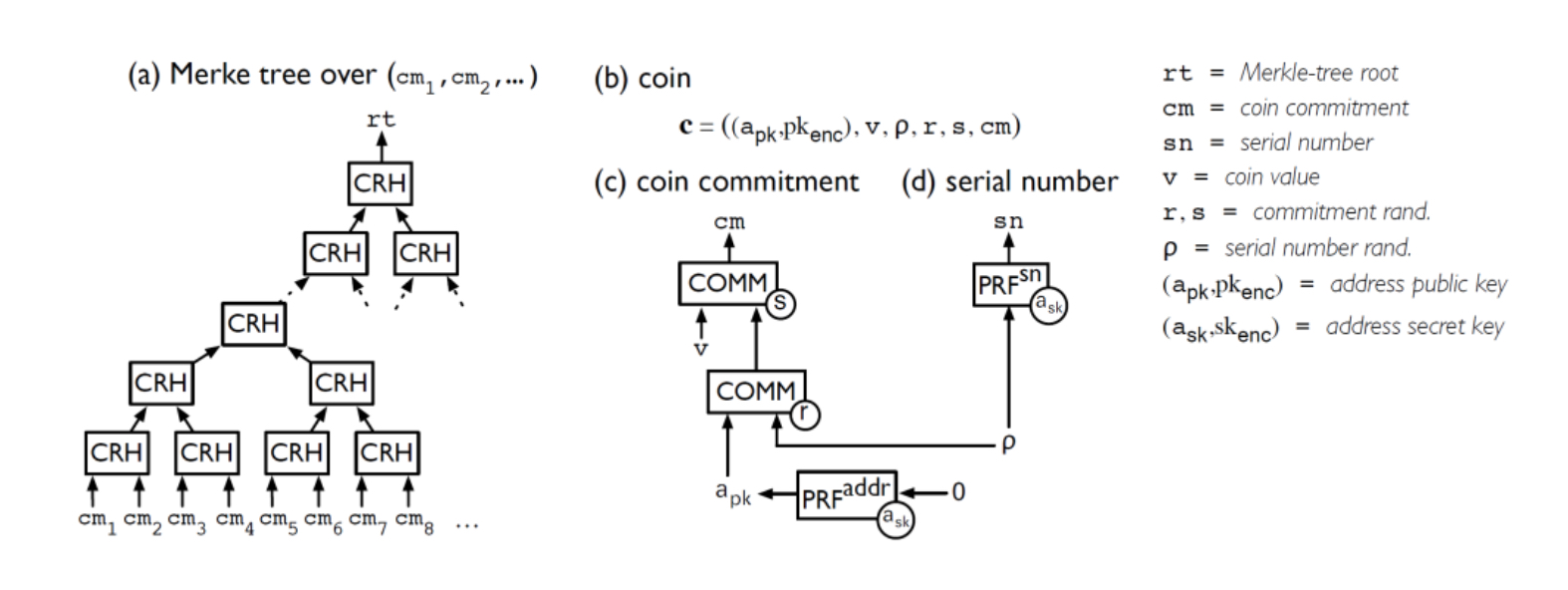
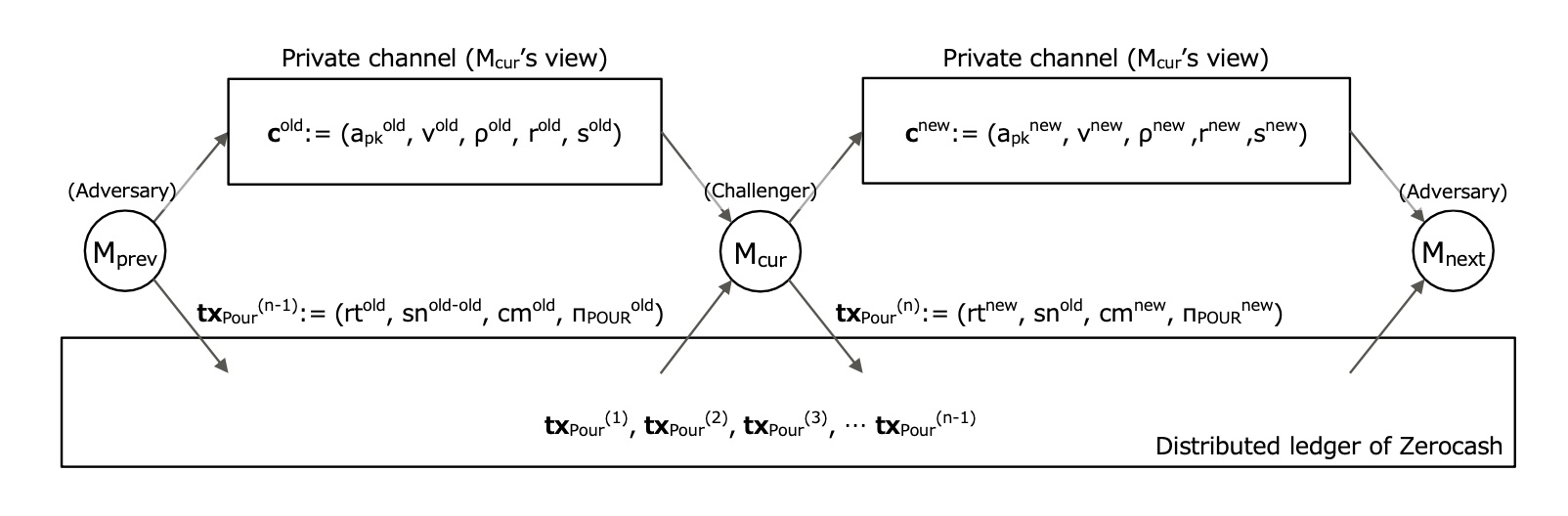
Fig. 13. Zerocash Coin Transfer System
To convince the recipient that the sent coins are valid (i.e., the shared secrets sent from the sender are well-formed), the sender includes a zero-knowledge proof πPOURnew in each transaction to prove that the identifiers and the secret parameters of sent coins are consistent, as shown in the followings (the suffixes are added from the viewpoint of the sender).
The coin commitment cmold is properly calculated from the secret information of the coin cold sent to and held by the sender.
The coin commitment cmnew is properly calculated from the secret information of the coin cnew produced by the sender and sent to the recipient.
The public key apkold used as an address when the sender has received cmold is properly generated from the sender’s secret key askold (the proof of the proper recipient apkold of cold).
The serial number snold is properly calculated from the secret information of the coin cold held by the sender and the sender’s secret key askold.
The secret information cmold is included in the CMList rtnew recorded in the shared ledger(the proof of the fact that cmold had already existed when the sender received the coin cold).
The total amount of old coins (v1old + v2old + ...) included in the transaction input is equal to the total amount of new coins (v1new + v2new + ...) included in the transaction output.
Preventing double-spending of the coin cold does not need to be proved using zero-knowledge proofs. It is sufficient to verify that snold has not yet appeared in any transaction input recorded in the shared ledger.
Next, we prove that Zerocash is a universal zero-knowledge coin transfer system in Theorem 6.1.
Theorem 6.1. Zerocash is a universal zero-knowledge coin transfer system.
[ Proof. ] Let Mz be a coin transfer system of Zerocash. We show that, for every probabilistic polynomial-time participants Mprev, Mcur, Mnext ∈ Mz, we can construct a universal simulator Mu∗ for the Zerocash’s POUR transaction, where the ensemble of Mcur’s outputs and the ensemble of Mu∗’s outputs are computationally indistinguishable, and the identical simulator Mu∗ that is only dependent on its self-inputs can be used for all Mcur ∈ Mz.
Note that we do not construct the simulator regarding the public output parameters and implementation-dependent parameters (see Zerocash paper12 for more details).
Public-outputs of Mu∗
CMList rtsim = CRH(rdsim); rdsim = rand() ∈ self-inputs of Mu∗ (Note that rand() is a pseudorandom number generator.)
CMList rtnew of Mcur’s public-outputs is a Merkle-tree root and thus a returned value of a collision-resistant hash function CRH(x) wherein x = ccroot = concat(CRH(cc0), CRH(cc1)) (cc0 and cc1 are other concatenated returned values of CRH(x)). Since CRH(x) is uniform, rtnew = CRH(ccroot) is computationally indistinguishable from rtsim = CRH(rdsim) that is only dependent on the self-inputs of Mu∗. Therefore, Mu∗ can universally simulate the public-output rtnew of Mcur.
Serial number snoldsim = PRF[askoldsim](ρoldsim ); askoldsim, ρoldsim = rand() ∈ self-inputs of Mu∗
Serial number snold of Mcur’s public-outputs is a returned value of a pseudo-random function PRF[askold](x) wherein x = ρold (a random value generated by Mprev), which is computationally indistinguishable from PRF[askold](x) wherein x = ρoldsim= rand() (a random value generated by Mu∗ as shown below). Furthermore, PRF[askold](ρold ) is also computationally indistinguishable from snoldsim= PRF[askoldsim](ρoldsim) where Mu∗ replaces askold with askoldsim (a secret key of Mu∗). Since snoldsim is only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the public-output snold of Mcur.
Coin commitment cmsim = COMMssim (vsim||COMMrsim (apksim||ρsim)); apksim = apknew, vsim = vnew, ρsim = ρnew, rsim = rnew, ssim = snew ∈ self-inputs of Mu∗
Coin commitment cmnew of Mcur’s public-outputs is a returned value of a commitment function COMMx(z) wherein x = snew denotes the commitment trapdoor, and z = vnew||COMMrnew (apknew||ρnew) denotes the committed value. Mu∗ can use the same coin commitment cmsim = cmnew as Mcur, because apksim = apknew, vsim = vnew, ρsim = ρnew, rsim = rnew, ssim = snew, as shown below. Since cmsim is only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the private-output cmnew of Mcur.
ZKP Sim[πPOURsim] = Sim[Prove(pkPOUR, x = (rtoldsim, snoldsim, cm old), a)]; rtoldsim, snoldsim, cmsim self-inputs of Mu∗
ZKP πPOURnew of Mcur’s public-outputs is a returned value of a zk-SNARK prove function Prove(pkPOUR, x, a) wherein x = (rtold, snold, cmnew) denotes an instance of the NP language L of the statement POUR, and a = (askold, cold, cnew) denotes a witness. Assuming that Mu∗ send a coin coldsim = (apkoldsim, voldsim, ρoldsim , roldsim, soldsim, cmoldsim), where apkoldsim is a public key of Mu∗, voldsim is larger than any assumed vnew, ρoldsim = rand(), roldsim = rand(), and soldsim = rand(), to itself in the past (before rtoldsim). Under this assumption, Mu∗ can generate a proof πPOURsim = Prove(pkPOUR, x = (rtoldsim, snoldsim, cmsim) , a) that meets completeness of zero-knowledge proof. πPOURnew and πPOURsim are computationally indistinguishable because their inputs are mapped to a set of exponent values in the proof of zk-SNARK proposed by Parno et al.14 Furthermore, πPOURsim is also computationally indistinguishable from its zero-knowledge proof simulator Sim[πPOURsim] that is not dependent on a. Since Sim[πPOURsim] is only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the private-output πPOURnew of Mcur.
Private-outputs of Mu∗
Address public key apksim = apknew ∈ self-inputs of Mu∗
Address public key apknew of Mcur’s private-outputs is a number. Mu∗ can use the same address public key apksim = apknew as Mcur. Since apksim is only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the private-output apknew of Mcur.
Coin value vsim = vnew ∈ self-inputs of Mu∗
Coin value vnew of Mcur’s private-outputs is a number. Mu∗ can use the same coin value vsim = vnew as Mcur. Since vsim is only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the private-output vnew of Mcur.
Randomly sampled values ρsim = ρnew = rand(), rsim = rnew = rand(), ssim = snew = rand() ∈ self-inputs of Mu∗
Randomly sampled values ρnew, rnew, snew of Mcur’s private-outputs are the random values generated by Mcur. Mu∗ can use the same random values ρsim = ρnew, rsim = rnew, ssim = snew as Mcur. Since ρsim, rsim, ssim are only dependent on the self-inputs of Mu∗, Mu∗ can universally simulate the private-outputs ρnew, rnew snew of Mcur.
Q.E.D.
Therefore, we finally conclude that Zerocash is CT-unlinkable from Theorem 5.1 and Theorem 6.1.
Unlinkability is a crucial property of cryptocurrencies that protects users from de-anonymization attacks. This paper first illustrated a privacy issue in Mimblewimble that could allow two colluded adversaries to merge a person’s two independent chunks of personally identifiable information (PII) into a single PII.
To analyze the privacy issue, we formulated unlinkability between two sets of objects and a privacy adversary model in cryptocurrencies called the counterparty adversary model. On these theoretical bases, we defined an abstract model of blockchain-based cryptocurrency transaction protocols called the coin transfer system, and unlinkability over it called coin transfer unlinkability (CT-unlinkability). Furthermore, we introduced zero-knowledgeness for the coin transfer systems to propose a method to easily prove the CT-unlinkability of cryptocurrency transaction protocols.
Finally, we proved that Zerocash is CT-unlinkable by using our proving method to demonstrate its effectiveness. It is also possible to utilize our proving method to design brand-new prospective CT-unlinkable anonymous cryptocurrencies in the future.
This work is partially supported by JSPS KAKENHI Grant Numbers 17KT0081 and 22H03589.
All authors contributed equally to this work.
All authors have affirmed they have no conflicts of interest as described in Ledger’s Conflict of Interest Policy.
1 Bonneau, J., Miller, A., Clark, J., Narayanan, A., Kroll, J. A., Felten, E. W. “SoK: Research Perspectives and Challenges for Bitcoin and Cryptocurrencies.” In 36th IEEE Symposium on Security and Privacy (S&P). 1 104–121 (2015) http://doi.org/10.1109/SP.2015.14.
2 Amarasinghe, N., Boyen, X., Mckague, M. “A Survey of Anonymity of Cryptocurrencies.” In Australasian Computer Science Week Multiconference (ACSW). 1 1–10 (2019) https://doi.org/10.1145/3290688.
3 Silveira, A., Betarte, G., Cristia, M., Luna, C. “A Formal Analysis of the Mimblewimble Cryptocurrency Protocol.” Sensors 21.17 5951 (2021) https://doi.org/10.3390/s21175951.
4 Jedusor, T. E. “Mimblewimble.” (2016) (accessed 19 August 2022) https://docs.beam.mw/Mimblewimble.pdf.
5 Poelstra, A. “Mimblewimble.” (2016) (accessed 22 July 2022) https://scalingbitcoin.org/papers/mimblewimble.pdf.
6 National Institute of Standards and Technology (NIST). “Guide to Protecting the Confidentiality of Personally Identifiable Information (PII).” (2010) (accessed 22 July 2022) https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-122.pdf.
7 Beam community. “Beam: The Scalable Confidential Cryptocurrency.” (2020) (accessed 22 July 2022) https://docs.beam.mw/BEAM_Position_Paper_0.3.pdf.
8 Pfitzmann, A., Hansen, M. “A Terminology for Talking About Privacy by Data Minimization: Anonymity, Unlinkability, Undetectability, Unobservability, Pseudonymity, and Identity Management.” (2010) (accessed 22 July 2022) http://www.maroki.de/pub/dphistory/2010_Anon_Terminology_v0.34.pdf.
9 Backes, M., Kate, A., Manoharan, P., Meiser, S., Mohammadi, E. “AnoA: A Framework for Analyzing Anonymous Communication Protocols.” In 26th IEEE Computer Security Foundations Symposium (CSF). 1 163–178 (2013) https://doi.org/10.1109/CSF.2013.18.
10 Androulaki, E., Karame, G. O., Roeschlin, M., Scherer, T., Capkun, S. “Evaluating User Privacy in Bitcoin.” In 17th International Conference, Financial Cryptography and Data Security (FC). LNCS 7859 34–51 (2013) https://doi.org/10.1007/978-3-642-39884-1_4.
11 Nakamoto, S. “Bitcoin: A Peer-to-Peer Electronic Cash System.” (2008) (accessed 22 July 2022) https://bitcoin.org/bitcoin.pdf.
12 Ben-sasson, E., et al. “Zerocash: Decentralized Anonymous Payments from Bitcoin.” In 35th IEEE Sympo- sium on Security and Privacy (S&P). 1 459–474 (2014) https://doi.org/10.1109/SP.2014.36.
13 Maxwell, G. “Confidential Transactions.” (2015) (accessed 22 July 2022) https://www.weusecoins.com/confidential-transactions/.
14 Parno, B., Howell, J., Gentry, C., Raykova, M. “Pinocchio: Nearly Practical Verifiable Computation.” In 34th IEEE Symposium on Security and Privacy (S&P). 1 238–252 (2013) https://doi.org/10.1109/SP.2013.47 .
15 Ben-Sasson, E., Chiesa, A., Tromer, E., Virza, M. “Succinct Non-Interactive Zero Knowledge for a von Neumann Architecture.” In 23rd USENIX Security Symposium. 1 781–796 (2014) https://www.usenix.org/conference/usenixsecurity14/technical-sessions/presentation/ben-sasson.
16 Groth, J. “On the Size of Pairing-Based Non-interactive Arguments.” In 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT). LNCS 9666 305–326 (2016) https://doi.org/10.1007/978-3-662-49896-5_11.
17 Goldreich, O. Foundations of Cryptography: Volume 1, Basic Tools. Cambridge: Cambridge University Press (2001).
18 Grin community. “Introduction to Mimblewimble and Grin.” (2017) (accessed 22 July 2022) https://github.com/mimblewimble/grin/blob/master/doc/intro.md.
19 Ruffing, T., Moreno-Sanchez, P. “ValueShuffle: Mixing Confidential Transactions for Comprehensive Transaction Privacy in Bitcoin.” 133–154 (2017) https://doi.org/10.1007/978-3-319-70278-0_8.
20 Zcash community “Zcash github.” (2019) (accessed 22 July 2022) https://github.com/zcash/zcash.
